数字逻辑 one
这是你👱🏻的亡🐏补牢 因为你👱🏻马上就要被🐏了
(里面的很多图片都是你👱🏻搞的别处的,必须声明一下防止被🐏,你👱🏻只是个搬运工 但是你👱🏻还是发表点看法)
数字逻辑基础
2️⃣进制、8️⃣进制、🔟进制和🔟6️⃣进制之间的转换

比如你👱🏻可以:

对于一些不能算尽的十进制小数转换,可以根据需要表示到一定位数
你👱🏻依稀记得二进制 八进制 十六进制这些多少沾点联系,有highway可走。


你👱对于8421BCD码稍微沾点陌生,以上你👱🏻大计基还学过,但是后面的你👱🏻估计要么是碎片清理了,要么就是本地没存过。
这个是🔟进制与8421BCD🐴转换

其实就是🔟进制一位换成8421🐴四位,你👱🏻确实无语凝噎了。
你👱🏻看书上讲了好几个🐴,所以这里来个总结:
编🐴
1.8421🐴
8️⃣421🐴指的是四位二进制数,从00001001,分别代表十进制09,其每位的权分别为2️⃣的三次方(8️⃣)、2️⃣的二次方(4)、2️⃣的一次方(2️⃣)、2️⃣的0次方(1)。四位二进制🐴的权重从左到右分别为8,4,2,1。类似的还有2421🐴,5421🐴。
比如5421🐴中:
9对应1100
8对应1011
5对应1000
2421🐴中:
9对应1111
8对应1110
5对应1011
2.余3️⃣🐴
是由8️⃣421码加3后形成的(即余3️⃣码是在8️⃣421码基础上每位十进制数BCD码再加上二进制数0011得到的)
比如:
8421中的0000 就变成了0011,
1001变成1100
必须补充说明下,你👱🏻才知道2421和余3️⃣🐴的对9自补是要考的重点,必须补充说明下了
对9自补是啥呢 就是说比如2421🐴只要自身按位变反,便可得到该数对9的2421🐴说
3.循环🐴
循环🐴的特点是任何2️⃣个相邻的代码只有一个2️⃣进制位的状态不同。
从某一编🐴变到下一相邻编🐴时,只有一位状态发生变化,译🐴时不会发生竞争冒险现象,这种编🐴是一种无权🐴
比如书上的余3️⃣循环🐴,其实余3🐴和余3️⃣循环🐴是different的,后者与格雷🐴多少沾点关系。
格雷🐴是相邻两位之间仅相差1,得到方法就是对原来的数的基础上相邻两位之间进行比较,如果两位之间不同,则得1,相同则得0,比较从右向左进行。
比如余3️⃣🐴到余3️⃣循环🐴:
(0)0110,
(4)3210
0,1位比较:1
1,2位比较:0
2,3为比较:1
3,4位比较:0
所以结果为0101
4.ASCII🐴
学计算机的不会不知道吧
十进制与原码、反码、补码之间的转换
这个你👱🏻看书上好像没有 但是万一呢
1.原🐴
就是2️⃣进制定点表示法,即最高位为符号位,”0“表示正,”1“表示负,其余位表示数值大小。

2.反🐴
正数的反🐴与其原🐴相同;负数的反🐴是对其原🐴逐位取反,但符号位除外。

3.补🐴
正数的补🐴与其原🐴相同;负数的补🐴是在其反🐴的末位+1。

逻辑门电路
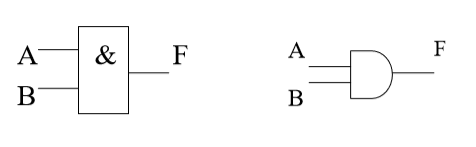
表达式:F=A*B=AB
你👱🏻:这是与🚪
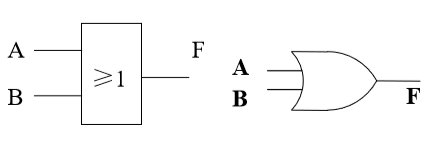
表达式:F=A+B
你👱🏻:这是或🚪

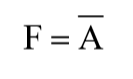
你👱🏻:这是非🚪
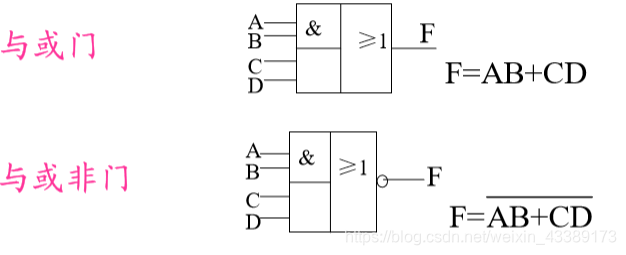
你👱🏻:这是复合逻辑🚪
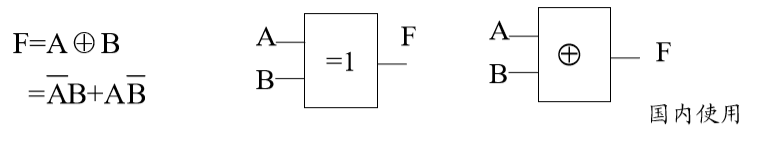
你👱🏻:这是异或🚪
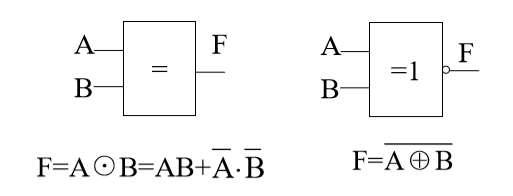
你👱🏻:这是同或🚪
逻辑代数运算法则

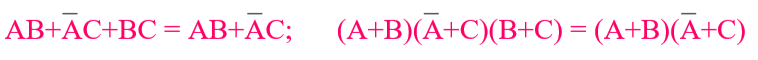
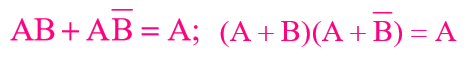

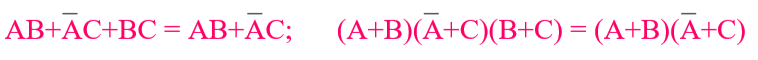
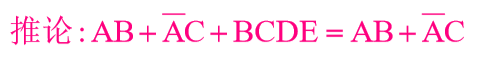
你👱🏻:都给你👱🏻记下来
至于怎么证明的你👱🏻就不print了,可以运用搜索引擎。
你👱🏻多少沾点心软还是给个网址
https://blog.csdn.net/wu_tongtong/article/details/104576536
逻辑代数基本规则
代换规则
任何含有变量X的逻辑等式,若将所有出现变量X的地方都用另一逻辑表达式Y代换,则等式仍然成立。使用代换规则时,要将等式两边所有出现被代替变量X的地方均代入同一表达式,否则等式不成立。你👱🏻觉得这个跟数学里面看做一个整体是一个art。
对偶规则
对于任何一个逻辑函数F,若将F表达式中所有的”*”和”+”互换,”0”和”1”互换,并保持运算顺序不变,则所得到新的函数称为函数F的对偶函数F’
你👱🏻:(A+B)(C+D)➡️AB+AC
反演规则
对于任何一个逻辑函数F,若将F表达式中所有的”*”和”+”互换,”0”和”1”互换,原变量和反变量,并保持运算顺序不变,则得到F反函数F’。
你👱🏻:

(有个符号你👱🏻打不出来多少沾点无奈)
逻辑函数的化简
公式法化简

你👱🏻:给你👱🏻记住,不然死🐴
卡诺图化简
1.逻辑函数最小项表达式
要说卡诺图,你👱🏻必须先提一嘴这个,不然你画你🐴
最小项是啥呢?就是一个函数的某个乘积项包含了函数的全部变量,其中每个变量都以原变量或反变量的形式出现,且仅出现一次,则这个乘积项称为该函数的一个标准积项,通常称为最小项。
你👱🏻知道光是这样说还不够clear,所以你👱🏻:
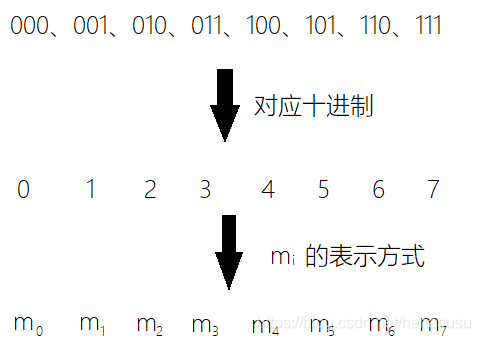
你👱🏻发现书上好像没有这个:
最小项的的相邻性:任何两个最小项如果他们只有一个因子不同,其余因子都相同,则称这两个最小项为相邻最小项。
例如:m0和m1具有相邻性,m1和m2却没有,因为他们有两个不同的因子;m3和m4也不相邻,但是m3和m2相邻。
相邻的两个最小项之和可以合并一项,消去一个变量。
比如:
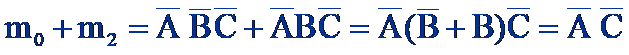
OK了马上炫酷起来
卡诺图:在这个方格图中,每一个方格代表逻辑函数的一个最小项,而且几何相邻(在几何位置上,上下或左右相邻)的小方格具有逻辑相邻性,即两相邻小方格所代表的最小项只有一个变量取值不同
对于有n个变量的逻辑函数,其最小项有2^n个。因此该逻辑函数的卡诺图由 2^n 个小方格构成,每个小方格都满足逻辑相邻项的要求。
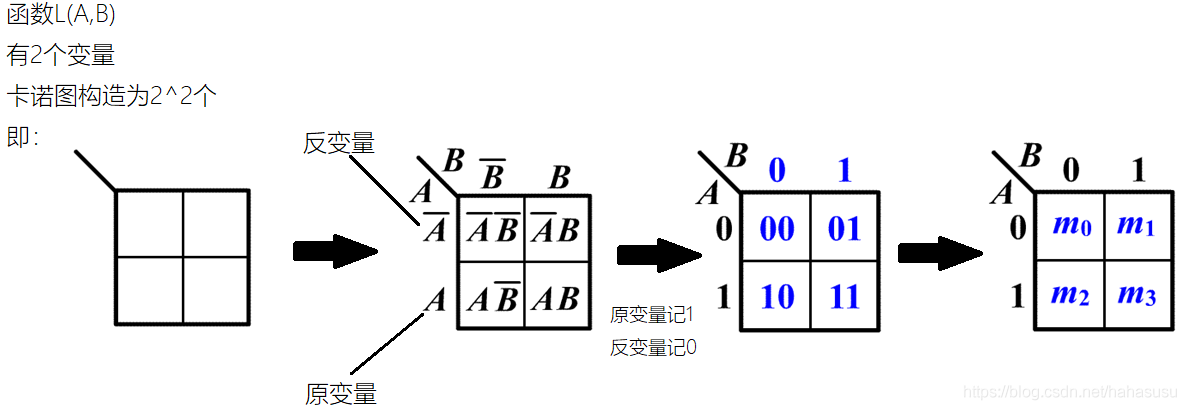
你👱🏻:这是两变量

你👱🏻:这是三变量
这个东西必须要化简才能沾点作用
卡诺图中两个相邻1格的最小项可以合并成一个与项,并消去一个变量。
卡诺图中四个相邻1格的最小项可以合并成一个与项,并消去两个变量。
卡诺图中八个相邻1格的最小项可以合并成一个与项,并消去三个变量。
你👱🏻:比如
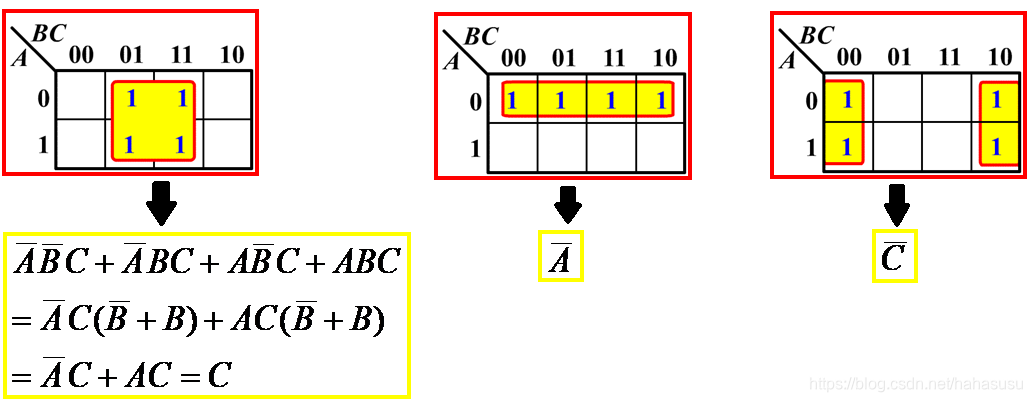
你👱🏻有这么几点需要明确:
列出逻辑函数的最小项表达式,由最小项表达式确定变量的个数(如果最小项中缺少变量,应按例的方法补齐)。
画出最小项表达式对应的卡诺图。
将卡诺图中的1格画圈,一个也不能漏圈,否则最后得到的表达式就会与所给函数不等;1格允许被一个以上的圈所包围。
圈的个数应尽可能得少。即在保证1格一个也不漏圈的前提下,圈的个数越少越好。因为一个圈和一个与项相对应,圈数越少,与或表达式的与项就越少。
按照2k个方格来组合(即圈内的1格数必须为1,2,4,8等),圈的面积越大越好。因为圈越大,可消去的变量就越多,与项中的变量就越少。
每个圈应至少包含一个新的1格,否则这个圈是多余的。
用卡诺图化简所得到的最简与或式不是唯一的
你👱🏻觉得万一不确定可以用🐷💰方法,就是硬算来保证下正确率
光是这样卡诺图视野还是不够清楚,所以你爹必须给点🐷💰示范:
❌1:多画一个圈

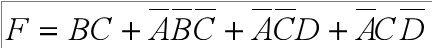
✔️:
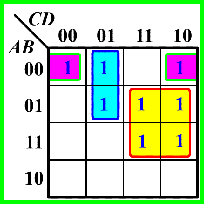

❌2:圈的不够大
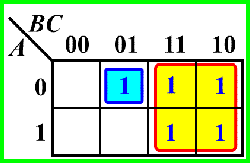
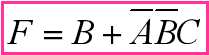
✔️:

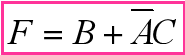
❌3:圈的不够大
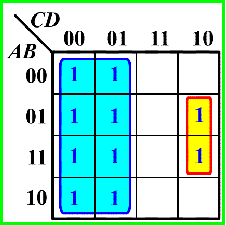
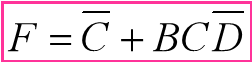
✔️:


❌4:有一个圈没有新的1格
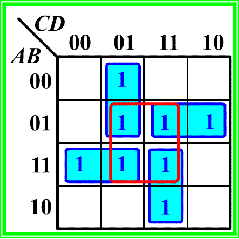

✔️:
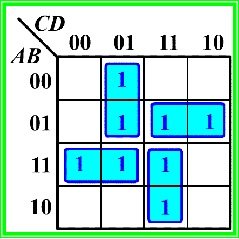
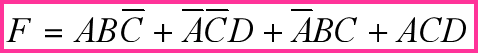
你👱🏻总结
逻辑函数的化简有公式法和卡诺图化简法等。
公式法是利用逻辑代数的公式和规则(定理)来对逻辑函数化简,这种方法适用于各种复杂的逻辑函数,但需要熟练地运用公式和规则(定理),且具有一定的运用技巧。
卡诺图化简法简单直观,容易掌握,但变量太多时卡诺图太复杂,一般说来变量个数大于等于5时该法已不适用。
在对逻辑函数化简时,充分利用无关项可以得到更为简单的结果。




